El parámetro de una elipse y la división por zero

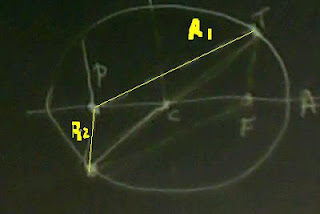
Para evitar dividir por cero si 2GM= 0, ó 2GM= R, en la conocida ecuación de Schwartschild, Einstein propuso un cambio de variables. En lugar de la distancia (R) al centro de un agujero negro, se usaría la distancia al horizonte de eventos. En el artículo ER(Einstein Rosen) se lee:

• u^2 = R—2GM

Lo que nadie comenta es que esta operación resuelve uno de los números de Christoffel, distinto al que es perpendicular a la superficie, que previamente pude calcular con el teorema de Gauss (¿el primer principio holográfico?), usando la distancia acortada(r).

u^2 coincide además con el parámetro (p) de una elipse que tiene por semiejes R y r.

Intuyo, sin otros argumentos que el agujero negro está en rotación por lo que la órbita es elíptica... y me pregunto si órbitas estrictamente circulares son siquiera posibles.

corregido 27/4/17

Nota: hay interesantes desarrollos respecto de los artículos ER y EPR (se agrega Podolsky)...

Kepler, sólo Geometría

En páginas previas se ve que puedo considerar a la excentricidad (e) de una elipse como tanhw, entonces coshw es energía. En el planeta Tierra, por ejemplo coshw se calcula dividiendo el radio ecuatorial (Recu) por el radio polar (Rpol), o éste por el parámetro.

En cualquier elipse, órbita o planeta o Galaxia, es decir elipse geométrica, no se requieren explicaciones múltiples para explicar el achatamiento...

(Recu * Rpol)/ distancia focal

resulta el "tiempo propio" (tau) geométrico, multiplicando éste por coshw resulta el Tiempo geométrico i.e la distancia del Centro de la elipse al pie de la tangente al parámetro  (p)

Equivale a Kepler : Area / momento angular = tiempo constante ...
pero sin factor 2 ni factor π, ni masa (o masa =1).

Además:
p = Recu / (coshw)^2
p: parámetro
se sigue que Recu/Rpol/p es una progresión

Para recuperar los valores astronómicos de la órbita o planeta, divido el tiempo geométrico (o debiera llamarlo elíptico?) por el tiempo orbital y uso el mismo factor multiplicado por la distancia focal para obtener el momento angular dividido por 2π.

Si le parece tedioso examinar esta propuesta, le sugiero empezar con el perfil de la Gran Piràmide, ya que en él, la distancia focal y el parámetro son iguales...

– la excentricidad, por supuesto sería phi = .618033989

Elipses, un enfoque hiperbólico

Resulta:

• distancia focal = momentum angular
• semieje mayor (horizontal) = distancia al Sol  (media) desde el Polo
• eje vertical = contracción de Lorentz del eje horizontal
• parámetro = contracción de Lorentz del eje vertical
• pie de tangente a un extremo del parámetro = Tiempo

Un cuerpo sólido que gira, una órbita, una galaxia, etc., se achatan verticalmente y se alargan
en el plano de rotación. El foco único del círculo se separa en dos en proporción al momento angular, es lo que se desprende del primer punto en la lista.

Tomando estos valores de la hipérbola y = x+1/x, todo calza exactamente.

En la órbita terrestre, la distancia del centro a un foco y al pie de la tangente tienen el mimo cuociente a los valores dinámicos conocidos...

Primero se debe identificar la excentricidad con una velocidad y por lo tanto una tangente hiperbólica.

Ejercicio para la órbita de la Tierra:

Divida 2.5E9 por 1.496E11, resulta la excentricidad = tanhw. Coshw será el factor gamma de Einstein y la relación entre los ejes y el parámetro!

Todo ésto en cualquier elipse, es Geometría.

Corceles veloces, trono de oro, y demás

en construcción... a modo de apuntes

• porqué esos caballos llegan antes?, son más veloces... o bien largaron antes de tiempo,
tiene que ver con la expansion acelerada del Universo y con nuestra conocida 
hipérbola: y= x+ 1/x

• se puede pasar de una hipérbola a una órbita elíptica, probablemente hacia ambos lados de una parábola, me refiero basando todo en la velocidad de escape, como hemos hecho aquí...

una tangente desde el eje X hasta el cruce del latus rectum con la órbita tendrá una pendiente numéricamente igual a la velocidad, incluso en la órbita terrestre!!! (si divido la velocidad por 2Π)
Además, la distancia del centro de la elipse a un foco es proporcional al momentum angular!

•Trono de Oro: en las tablillas de Venus aparece esta frase que se encuentra también en un registro del año octavo del Rey Ammizaduga. En la Cronologia Media sería el año —1638 A. de C.
La Nasa publica un Tránsito de Venus para tres años antes —1941 A de C... En las tablillas se apunta para Mayo de ese año  una conjunción inferior del planeta Venus con la Tierra, lo que por lo menos no es contradictorio
En —1638 antes de Cristo, software comercial (varios) ponen un tránsito de Venus aún más cercano con zero ° de separación angular... Usted llamaría al fenómeno de ver la sombra de Ishtar exactamente por delante del centro refulgente del Rey Sol, el "año del Trono de Oro".
El registro anual todavía existe y parece hablar de un trono de oro rojizo que se dedica en un Templo... como sea me sirve como nemmónico.

•La línea 2-8-28-32-50 se encuentra en la Tabla Periódica de Elementos y además refleja la relación de Kepler entre el cubo del radio y el cuadrado del Tiempo. Cada número de la línea es igual a
2T^2, también extensible al Sistema Solar

El número 16 se relaciona directamente con la hipérbola subyacente

continuará...