A fin de cuentas, creo que hay curvas con propiedades probabilísticas, como la curva de Gauss y otras.
La hipérbolas que presentaré luego facilitan enormemente cálculos de relatividad especial y general y de teoría cuántica a un nivel todavía sin límites..
Además de las que se ven, una tercera es la hipérbola unitaria x^2 – y^2 =1 donde se registran la energía (coshw) y momentum (sinhw) correspondiente a una velocidad relativa
tanhw que es y/x en la curva
x^2 —y^2 = 1;
pero x/y en la primera curva donde
x= x + 1/x
es difícil de creer que todo se puede definir escogiendo un solo número entre 0 y 1, que se resta de 1.
Pero, es más práctico escoger cualquier número como 2GM y otro mayor como X; para empezar, el producto de ellos es el cuadrado del momento angular y el cuociente es el cuadrado de la velocidad de escape. Lo fascinante, para mí es que no se requiere una dirección determinada para que a esta velocidad un móvil abandone un campo gravitacional dado por 2GM.
Hay bastante más, pero suficiente por ahora...
martes, 31 de mayo de 2016
viernes, 20 de mayo de 2016
Global vs. local... o todo lo contrario
Teorema básico (relatividad):
• para 2 eventos en espacio-tiempo con un intervalo espacial, siempre existe un marco de referencia en que son simultáneos...
Creo que es lo que se ve en la hipérbola del grabado (en verde)
Eje de las Y= tiempo
Eje de las X= espacio
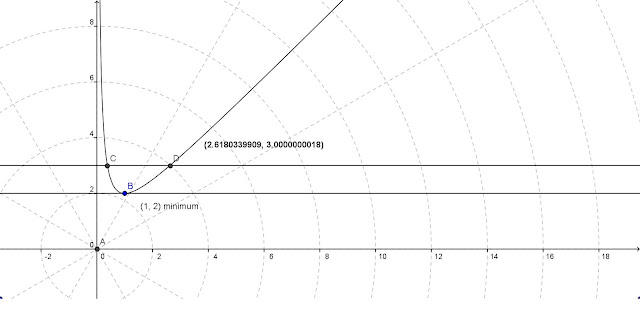
hipérbola verde = x+1/x
intervalo espacial= más horizontal que vertical, i.e < de 45°
Se implica que los dos eventos están entrelazados ("entangled") instantáneamente a pesar de estar fuera de alcance causal, aún a la velocidad de la luz.
Las velocidades x/y en 2 puntos horizontales entre sí suman 1 ...
por lo que actúan como probabilidades cuánticas y como particulas relativistas
En breve y a pesar de todo; este tema puede llevar al desarrollo de un campo que comprenda teoria de relatividad y teoria cuántica.
Nótese que si el cono de luz se dibuja desde el origen, todo es causal, y no hay "entanglement". Es decir, habría un retraso en que desde el vacío surja una partícula en el punto B (mínimum) con suficiente energía para emitir un par partícula/antipartícula en direcciones opuestas.
1/x puede ser la curvatura de un círculo de radio x, la derivada del ln(x), el punto en que la velocidad es 1—v en relación a la velocidad en x... y aparece en muchas otras cosas, como la fórmula para calcular el efecto Doppler relativista, etc.
• para 2 eventos en espacio-tiempo con un intervalo espacial, siempre existe un marco de referencia en que son simultáneos...
Creo que es lo que se ve en la hipérbola del grabado (en verde)
 |
| estan marcadas las lineas y = 3, e y = 2 |
Eje de las X= espacio
hipérbola verde = x+1/x
intervalo espacial= más horizontal que vertical, i.e < de 45°
Se implica que los dos eventos están entrelazados ("entangled") instantáneamente a pesar de estar fuera de alcance causal, aún a la velocidad de la luz.
Las velocidades x/y en 2 puntos horizontales entre sí suman 1 ...
por lo que actúan como probabilidades cuánticas y como particulas relativistas
En breve y a pesar de todo; este tema puede llevar al desarrollo de un campo que comprenda teoria de relatividad y teoria cuántica.
Nótese que si el cono de luz se dibuja desde el origen, todo es causal, y no hay "entanglement". Es decir, habría un retraso en que desde el vacío surja una partícula en el punto B (mínimum) con suficiente energía para emitir un par partícula/antipartícula en direcciones opuestas.
1/x puede ser la curvatura de un círculo de radio x, la derivada del ln(x), el punto en que la velocidad es 1—v en relación a la velocidad en x... y aparece en muchas otras cosas, como la fórmula para calcular el efecto Doppler relativista, etc.
jueves, 14 de abril de 2016
Trayectorias sobre un paraboloide
"Un número en cada punto del espacio, ésto es un Campo".
Richard Feynman
"Teaching an advanced course on Theoretical Physics may just consist on studying the Harmonic Oscillator, over and over, from all possible points of view"
Sidney Coleman
Ejercicio básicoSobre un vaso o cuenco de greda de forma paraboloide haga un corte vertical. Separando los pedazos, se podrán calzar el uno al fondo del otro. Esto ocurre aún si el corte no coincide con el eje de simetría.
Compare con una esfera. Si el corte no pasa por el centro, no describe un círculo máximo y por ende no calzarán los pedazos.
Métrica: ||x — y|| distancia entre dos vectores
El número 45 de la espiral es triangular y además la suma de cuadrados de otros dos triangulares ya que pertenece a la secuencia 1,10,45,136,325. Esto permite usar números enteros en lo que sigue.
45= 6^2 +(– 3)^2
65= 7^2 +(– 4)^2
89= 8^2 +(– 5)^2 ,etc
Estos números están alineados como las alas de un pájaro a partir del 45 en paralelo a los arcos
6,14,26,42 y 6,16,30,48
y a todos los otros arcos que ocupan cada cuadrante, son espirales hiperbólicas perfectas (sorpresa para mí)
Ej: 1,7,17,31,etc.
3,11,23,39, etc.
El corte:
A altura 65 un corte vertical tiene la forma de la parábola 2x^2 pero deplazada verticalmente en 4.5 y el ancho de la curva llega a –4 y 7
d=7– –4 =11
aplicando un antiguo procedimiento de Mesopotamia
5.5^2— (–4*7*cos 180°)= 1.5^2
1.5 +5.5=7
1.5 –5.5=(–4)
Pregunta : ¿cómo llamar un espacio que tiene métrica, producto escalar de vectores, desigualdad de triángulos y regla del paralelograma(*nota)?....
Mientras Ud. lo piensa, yo persevero en examinar la superficie de un paraboloide elíptico... numerado.
Apoyo logístico para construir la Gran Pirámide
Descarto poder trasladar el ángulo basal de la pirámide, peldaño a peldaño, 203 veces y lograr evitar errores. De ahí que mi propuesta (ver páginas previas) tiene sentido.
Para ello:
•dibujar un cuadrado con la mitad del área de otro dado ya aparece en tablillas de geometría en arcilla en Mesopotamia de unos 2000-3000 años de antigüedad
•empezar a construir el perímetro del cuadrado interno, por las esquinas
–ésto es lo fundamental, se va a erigir un cuerpo central en forma de caja, usando su espacio interno con estructuras que permitan izar los bloques de piedra—
•un frustrum de pirámide se puede descomponer en un cuerpo central en forma de caja, 4 prismas laterales y cuatro pirámides de esquina. Un libro chino que posiblemente sobrevivió a la quema de libros que hizo Shi Huang Ti (3S. A. de C.), describe esta disección.
•los egipcios inventaron el uso de 1/tan para describir un ángulo
•los egipcios inventaron el remen que es un cúbito imperial multiplicado por √2
•Un constructor británico ha demostrado el uso de palancas como se ven en grabados egipcios.
•Se han encontrado artefactos como "hamacas" que podrían ayudar a izar piedras, cambiando su centro de gravedad.
•la Gran Galería pudo servir como funicular usando los conocidos rieles laterales
•ya existe la idea de flotar las piedras en el Nilo para acercarlas quizás hasta la misma Pirámide en tiempos de crecida
Para ello:
•dibujar un cuadrado con la mitad del área de otro dado ya aparece en tablillas de geometría en arcilla en Mesopotamia de unos 2000-3000 años de antigüedad
•empezar a construir el perímetro del cuadrado interno, por las esquinas
–ésto es lo fundamental, se va a erigir un cuerpo central en forma de caja, usando su espacio interno con estructuras que permitan izar los bloques de piedra—
•un frustrum de pirámide se puede descomponer en un cuerpo central en forma de caja, 4 prismas laterales y cuatro pirámides de esquina. Un libro chino que posiblemente sobrevivió a la quema de libros que hizo Shi Huang Ti (3S. A. de C.), describe esta disección.
•los egipcios inventaron el uso de 1/tan para describir un ángulo
•los egipcios inventaron el remen que es un cúbito imperial multiplicado por √2
•Un constructor británico ha demostrado el uso de palancas como se ven en grabados egipcios.
•Se han encontrado artefactos como "hamacas" que podrían ayudar a izar piedras, cambiando su centro de gravedad.
•la Gran Galería pudo servir como funicular usando los conocidos rieles laterales
•ya existe la idea de flotar las piedras en el Nilo para acercarlas quizás hasta la misma Pirámide en tiempos de crecida
martes, 22 de marzo de 2016
Más sobre la pirámide de Keops
 |
| Arco DD' es común a los ángulos Alfa (central) y Beta ( inscrito) |
Esto se puede aplicar a una pirámide, la ladera de un cerro, la Torre de Pisa, etc., pero se aprecia que una pared o edificio vertical no es más que un caso particular aplicable.
En Giza A representa el pie del apotema lado Este, B es la entrada al Templo Mortuorio y D' es el nivel en que se encuentra la Cámara del Rey sobre esa cara lateral de la Gran Pirámide.
AB=AD' ambos miden aprox. 179,1384 ft. como registra Flinders Petrie en su obra.
No he podido encontrar esta útil noción en manuales de exploradores o de topografía de campaña.
En la página previa uso esta idea para proponer un plan de construcción de la Gran Pirámide que presenta ventajas obvias sobre otros métodos.
En Giza A representa el pie del apotema lado Este, B es la entrada al Templo Mortuorio y D' es el nivel en que se encuentra la Cámara del Rey sobre esa cara lateral de la Gran Pirámide.
AB=AD' ambos miden aprox. 179,1384 ft. como registra Flinders Petrie en su obra.
No he podido encontrar esta útil noción en manuales de exploradores o de topografía de campaña.
En la página previa uso esta idea para proponer un plan de construcción de la Gran Pirámide que presenta ventajas obvias sobre otros métodos.
Suscribirse a:
Entradas (Atom)